FPS游戏绘制(一)

FPS类型游戏的设计研究和游戏安全,反外挂研究

学习这套课程的基础包含少量的汇编知识和编程知识,

一定的数学知识和内存知识

基础建立在 任鸟飞2020课程 前100课的前提下即毫无压力的学习.

当然我们要从最简单的概念开始学习,请勿急躁

这个课题本着最简单易懂,从本质完全解析的态度,所以有任何细节不懂,哪怕是三角函数,都可以找我探讨

向量

可能大家问为什么要学习向量, 原因是向量是矩阵的元素,而矩阵是帮助我们快速计算的朋友

所以就算不能完全掌握,了解一下是必要的.

指具有大小和方向的量.

一维向量,例如 1 对应的就是从0到1的向量,大小是1,方向X正轴方向

我们说向量只有大小和方向, 不存在其他属性,所以 一维向量 1 也可以表示 从1到2 从-1到0

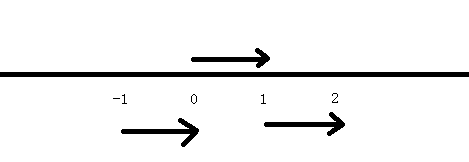
向量可以进行算数运算的.例如 1+1 =2 2个大小是1,方向X正轴方向的向量

相加等于1个大小是2,方向X正轴方向的向量

1*3 = 3 给向量放大3倍

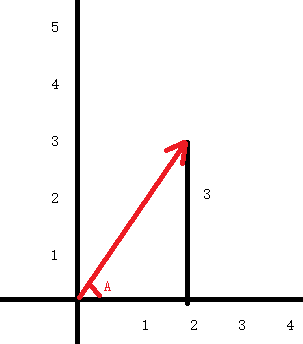
二维向量,例如 2,3 书写格式为[2,3]

对应的是 从原点0,0 到 坐标 2,3 的向量, 大小就需要计算了

根据三角函数,大小等于 sqrt(22+33) ,同样这也是计算 二维空间2点的距离公式

(三角函数:直角三角形,斜边的平方 = 底边平方+高平方 , 知道任意2边可以计算出另外一个边的长度)

距离 = sqrt((X1-x2)(X1-x2)+(y1-y2)(y1-y2));

方向如图所示,我们下面再讲

向量只有大小和方向,同样二维向量 [2,3] 也可以表示 从3,0到5,3 ,可以任意位置开始

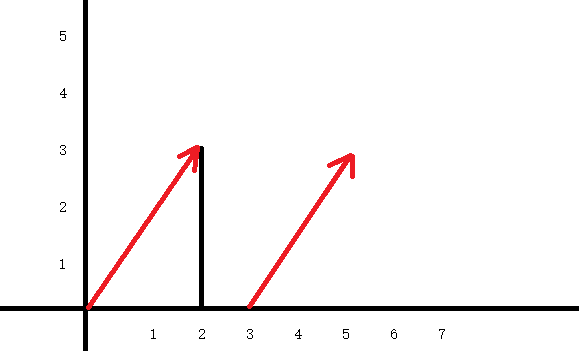
二维向量也可以进行算数运算.

例如 [2,3]+[2,1] = [4,4]

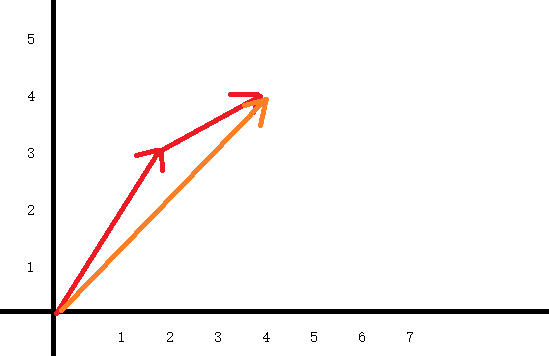
向量的乘法 [2,3]*[3,3] = 6+9= 15 向量的内积

向量的减法可以把空间2点的绝对坐标转化为相对坐标

[X1,Y1] - [X2,Y2]= [X1-X2, Y1 - Y2],相当于把向量移动到原点

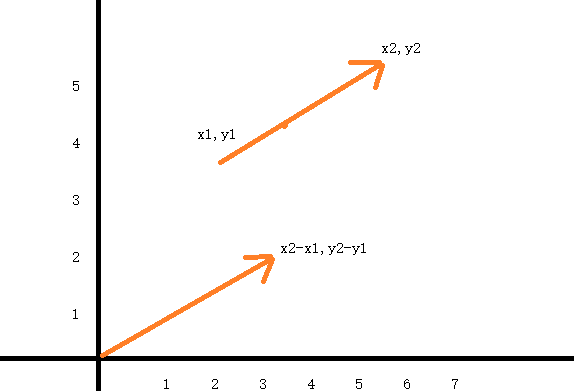
三角函数角度的问题

在游戏图像计算中角度是必不可少的部分

例如 我们知道了,如下三角形 高为3 底边为2

那么tanA = 3/2 我们想求A的角度怎么办呢? C++给我们提供API函数

A = atan(3,2); 这样就计算出来 A的角度了

不过atan()的返回值是弧度,我们如果想转为真正的角度 还是需要转换的

什么是弧度呢?你可以简单的理解为 正常角度如果是0-180的话 弧度就是 0- π

那么 atan(3,2) *180 / π 就把弧度转换成角度了

最终

A = atan(3,2)*180 / π;

另外一种情况,

知道了角度,想求边长

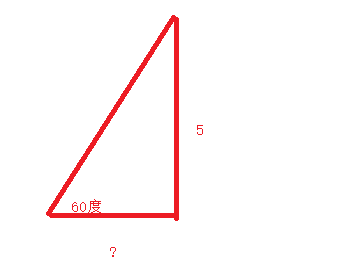
例如一个向量[?,5] 角度是东偏北 60度

我们怎么计算向量值呢?

很简单,

tan 60 = 5/底边

底边 = 5/ tan60,当然这里的角度参数也是弧度 ,如果你的是真实角度,我们又要把角度转换成弧度

最终

底边 = 5 / tan (60*π/180) ;

其他的 sin cos 也是同理,我们不是学习数学,所以暂时了解即可,后面用到再说.

三维向量

例如 2,1,3 格式[2,1,3]

向量写成行 或则列都可以

行向量 [2,1,3]

列向量

[ 2

1

3 ]

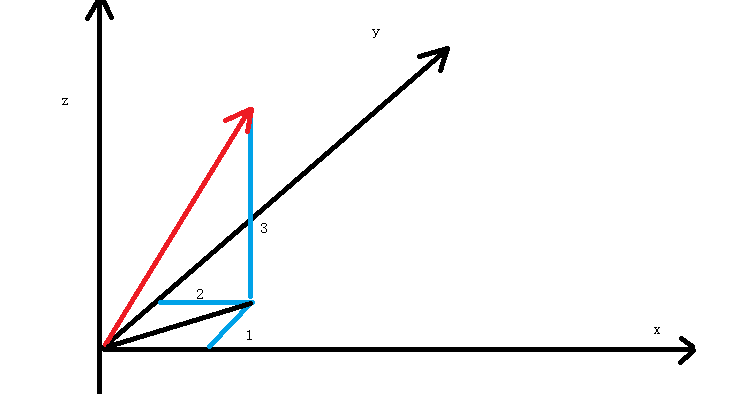
三维向量对应的是三维空间 2,1,3对应的是x,y,z

(注: 三维坐标系,很多书本是Y 为高度轴,切记X,Y,Z只是个符号,你可以起名叫a b c 也没问题

调转一下坐标系X,就变成了Y ,所以没有区别,不要死记名字,按照自己习惯来)

[2,1,3]就是从原点到坐标2,1,3的向量

大小计算就更加复杂一点了

先看懂下图的辅助线

根据三角函数,向量的大小等于 sqrt(11+22+3*3) ,同样这也是计算 三维空间2点的距离公式

距离 = sqrt((X1-x2)(X1-x2)+(y1-y2)(y1-y2)+(z1-z2)*(z1-z2));

而方向不再单纯是一个角度了,他包含水平角度 和 高低角度,这个我们后面再讲

向量的减法可以把三维空间2点的绝对坐标转化为相对坐标

[X1,Y1,Z1] - [X2,Y2,Z2]= [X1-X2, Y1 - Y2,Z1-Z2],相当于把向量移动到原点

同样三维向量也可以进行 加法 乘法等运算

例如[X1,y1,z1] * [1,2,3] = X1+y12+z13 向量的内积

到这里是不是对几何和线性代数的基础知识不再陌生了,其实就这点东西,很简单.

矩阵

为什么要学习矩阵,对于我们研究的课题来说,就是为了方便计算以及精准计算的,当然你可以不用.

多个向量组合成一个矩阵

矩阵可以看做一个特殊的向量，而向量也可以看做一个特殊的矩阵。

只有一行的矩阵 为行向量 行矩阵

只有一列的矩阵 为列向量 列矩阵

格式为 行*列

例如 3*3 矩阵:

1 2 3

5 7 1

2 2 1

例如 3*4 矩阵

1 2 3 5

5 7 1 1

2 2 1 2

同形矩阵 可以相加减(毕竟如果不是同型的话,没有办法对应相加减 这很好理解)

稍微有点难度的是矩阵相乘除

那么大家要注意的是:

1.矩阵是 多个向量的组合,矩阵的乘除就是 向量的乘除,而不是单独元素的乘除

2.两个矩阵相乘,用第一个矩阵的行 乘 第二个矩阵的列的方式 计算

由于使用方法的区别 AB != BA 而且 A* 不同的矩阵 结果可能相同

3.计算结果的存放

例如 2个2*2 矩阵相乘

第一行*第一列 放到 第一行第一列

第一行*第二列 放到 第一行第二列

第二行*第一列 放到 第二行第一列

第二行*第二列 放到 第二行第二列

a1 a2 乘 b1 b2 = a1b1 + a2b3 a1b2 + a2b4

a3 a4 b3 b4 a3b1 +a4b3 a3b2 + a4b4

mn 矩阵 和 ij 矩阵 由于是行 *列 所以

mn 矩阵一行的元素 要和 ij 矩阵一列的元素 必须相同

也就是 n == i

主要满足这个条件就可以相乘 否则不可以

矩阵特性

矩阵对于我们来说就是为了方便计算而生,并不是无可取代

举个例子

只有对角线为1 其他都是0的矩阵 单位矩阵

1 0 0 0

0 1 0 0

0 0 1 0

0 0 0 1

任何矩阵乘以 单位矩阵都为原来矩阵 把 1换成2 就是 放大2倍

比你一个元素一个元素的*2方便很多吧?

矩阵取一列

1 0 0 X 乘 0 = X 取X Y Z 向量

0 1 0 Y 0 Y

0 0 1 Z 0 Z

0 0 0 1 1 1

单独放大某个元素

X 0 0 0 乘 0 = 0 Z 扩大10倍

0 Y 0 0 0 0

0 0 Z 0 10 10Z

0 0 0 1 1 1

矩阵的乘法可以实现很多的功能

看起来是不是很方便,很强大?!

不借助矩阵把游戏坐标转换成屏幕坐标

无论是在窗口上绘制窗体,还是画各种方框,最核心的功能就是在于如何把游戏坐标也就是世界坐标转换成屏幕坐标.

这里我们先不借助于强大好用的矩阵,单纯用几何算法转换一下坐标

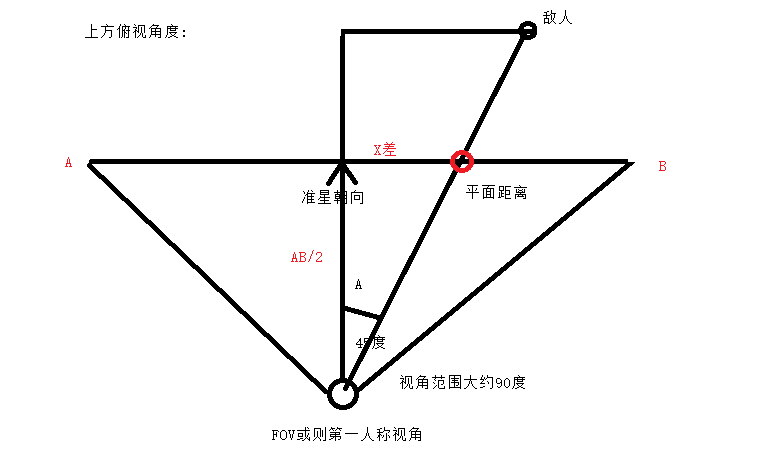
图看起来有点乱,我们慢慢来

这是游戏 上方俯视的平面图:

如果有不懂可以加我Q2217777779,会尽力帮助解答

1.水平可视角度 一般为90度, 也就是FOV 或则第一人称视角

但是这个值只是约值,可能不精准也是导致后面不精准的原因之一

2.我们准星一直在屏幕正中心的,所以向前做一个垂线,左右各45度

3.我们把三角形补全,等腰三角形的斜边就是我们的可视范围,任何游戏中的物品 敌人和我们的连线只有和这个斜边有交单才会显示到我们的屏幕中

如图中敌人和我们连线 焦点就是红色圆圈

4.角度A 可以根据具体朝向值简单分析出来,后面数据分析的时候再说

5.红色圆圈 在 AB 这条线上的位置

就是敌人在我们屏幕X坐标的等比例位置

所以这样就可以计算出来 屏幕坐标X了

tanA = X差/ (AB/2);

那么 X差 = tanA*(AB/2);

X差/(AB/2) = 屏幕坐标差/ (分辨率_宽度/2)

继续替换

tanA = 屏幕坐标差/ (分辨率_宽度/2)

角度还要转换一下成弧度

最终

屏幕坐标差 = tan(A*π/180) *(分辨率_宽度/2);

屏幕坐标 = 屏幕坐标差 + 分辨率_宽度/2;

int 水平差 = (int)(tan(水平角度差 * 3.1416 / 180) * ((m_分辨率宽) / 2));

屏幕坐标.x = (float)(m_分辨率宽 / 2 + 水平差);

屏幕坐标.y 也是同样的计算方法,不过屏幕宽高是不相同的,所以可视角也是有区别的

屏幕分辨率_高/屏幕分辨率_宽 = 高低可视角度 / 水平可视角度

int 高度差 = (int)(tan(高低角度差 * 3.1416 / 180) * ((m_分辨率宽) / 2));// 这里也是m_分辨率宽

因为可视角度不是45了,而是分辨率计算出来的角度

屏幕坐标.y = (float)(m_分辨率高 / 2 + 高度差);

最终代码如下:

bool 绘制::世界坐标转屏幕坐标_非矩阵(坐标结构_2& 屏幕坐标, FLOAT 水平角度差, FLOAT 高低角度差)

{

取窗口信息();

FLOAT 高低可视角度 = (FLOAT)((double)atan2(m_分辨率高, m_分辨率宽)*180/3.1415);

if (fabs(水平角度差) > 45 || fabs(高低角度差) > 高低可视角度)

{

return false;// 不在屏幕范围内

}

int 水平差 = (int)(tan(水平角度差 * 3.1416 / 180) * ((m_分辨率宽) / 2));

屏幕坐标.x = (float)(m_分辨率宽 / 2 + 水平差); i

nt 高度差 = (int)(tan(高低角度差 * 3.1416 / 180) * ((m_分辨率宽) / 2));

屏幕坐标.y = (float)(m_分辨率高 / 2 + 高度差);

return true;

}

但是我们发现这样计算出来的画框 是不精准的

主要2个原因一个是角度是约值,一个是计算过程中数值的溢出,尽量使用double 可以减少

也可以通过微调度数等等的方式 把他修正比较准确.

好我们下节课再见

参考视频:

链接: https://pan.baidu.com/s/1dN63zxgQECeeH1lzQ1P9cg 提取码: dgs9